the statistics of Secret Santa
- Written by Rheanna Mainzer, Melbourne Early Career Academic Fellow (Statistics Tutor), University of Melbourne
Last Christmas, my family gathered to organise our Kris Kringle. My sister drew her husband, but they were already buying presents for each other, so we decided to draw again. No one in my family (except me) is particularly interested in mathematics or statistics, but my brother fatefully asked:
What are the chances that all the partners draw each other?
At the time, my family consisted of eight people: my mother and her partner, my older sister and her husband, my younger brother and his new girlfriend, my grandpa (widowed and never remarried), and me (I was single). So there were three sets of partners and two singles.
I started thinking out loud about how to answer my brother’s question. One way to find a probability is to calculate the fraction
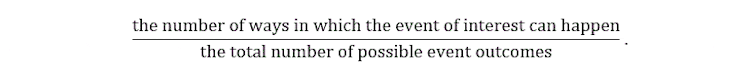 The “event of interest” here is that all three partners draw each other’s names and, because there are no other possibilities, my grandpa and I draw each other. This can only happen in one way, so the top line of the fraction above must be 1.
The “event of interest” here is that all three partners draw each other’s names and, because there are no other possibilities, my grandpa and I draw each other. This can only happen in one way, so the top line of the fraction above must be 1.
 My grandpa unwrapping his new weed sprayer on Christmas day.
Author provided
What’s the bottom line?
Unfortunately, the bottom line is much trickier to calculate. You want to count the total number of ways that eight people can draw names from a hat, without drawing themselves. For example, one possible event outcome is: I draw my mum, who draws my brother, who draws my sister, who draws her husband, who draws my brother’s new girlfriend, who draws mum’s partner, who draws my grandpa, who draws me.
My brother’s new girlfriend interrupted my thinking by asking whether the answer isn’t simply eight factorial (which is written in mathematical notation as “8!”).
For those who aren’t familiar,
My grandpa unwrapping his new weed sprayer on Christmas day.
Author provided
What’s the bottom line?
Unfortunately, the bottom line is much trickier to calculate. You want to count the total number of ways that eight people can draw names from a hat, without drawing themselves. For example, one possible event outcome is: I draw my mum, who draws my brother, who draws my sister, who draws her husband, who draws my brother’s new girlfriend, who draws mum’s partner, who draws my grandpa, who draws me.
My brother’s new girlfriend interrupted my thinking by asking whether the answer isn’t simply eight factorial (which is written in mathematical notation as “8!”).
For those who aren’t familiar,
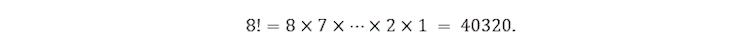 My family let out a collective “ooooooh!” at what they perceived as a challenge to my mathematical prowess from my brother’s new girlfriend.
Her guess was sensible but not quite right, because it included the outcomes in which someone draws their own name.
Without pen or paper handy I decided to file the problem away in the back of my mind and rejoin the conversation, which had swiftly moved on.
When in doubt, bring in the experts
I found the perfect place to resurrect this problem, at a recent MathsCraft event, which brought mathematicians, teachers and students together to explore problems like a research mathematician.
My University of Melbourne colleagues TriThang Tran, Sam Povall and Rhys Bowden are all experts in different mathematics research fields. I couldn’t think of anyone more qualified to count things than these three – surely they must be able to answer my Christmas conundrum.
However, a short brainstorm session revealed that the Kris Kringle question is harder than initially expected.
But lo, a possible saviour was delivered unto us in the form of Professor Nigel Bean, an expert in applied probability. Like the star guiding the Three Wise Men, hopefully Nigel would be able to guide us puzzled mathematicians to the solution.
“That’s easy!” Nigel confidently announced. But seconds later, his face fell as he too came to the realisation that this problem is deceptively difficult.
We threw ideas around the table, our voices rising in excitement. This captured the attention of two secondary school maths teachers, Amy Xue and Callum Johnson, who came over to investigate. While Sam brought Amy and Callum up to speed, Nigel and Rhys worked on the whiteboard, drawing tables and defining notation to help them. TriThang took a different approach, working at the table and using pictures to illustrate different outcomes.
My family let out a collective “ooooooh!” at what they perceived as a challenge to my mathematical prowess from my brother’s new girlfriend.
Her guess was sensible but not quite right, because it included the outcomes in which someone draws their own name.
Without pen or paper handy I decided to file the problem away in the back of my mind and rejoin the conversation, which had swiftly moved on.
When in doubt, bring in the experts
I found the perfect place to resurrect this problem, at a recent MathsCraft event, which brought mathematicians, teachers and students together to explore problems like a research mathematician.
My University of Melbourne colleagues TriThang Tran, Sam Povall and Rhys Bowden are all experts in different mathematics research fields. I couldn’t think of anyone more qualified to count things than these three – surely they must be able to answer my Christmas conundrum.
However, a short brainstorm session revealed that the Kris Kringle question is harder than initially expected.
But lo, a possible saviour was delivered unto us in the form of Professor Nigel Bean, an expert in applied probability. Like the star guiding the Three Wise Men, hopefully Nigel would be able to guide us puzzled mathematicians to the solution.
“That’s easy!” Nigel confidently announced. But seconds later, his face fell as he too came to the realisation that this problem is deceptively difficult.
We threw ideas around the table, our voices rising in excitement. This captured the attention of two secondary school maths teachers, Amy Xue and Callum Johnson, who came over to investigate. While Sam brought Amy and Callum up to speed, Nigel and Rhys worked on the whiteboard, drawing tables and defining notation to help them. TriThang took a different approach, working at the table and using pictures to illustrate different outcomes.
 Mathematicians working on the Kris Kringle problem together. From left to right: Nigel, Rhys, Sam, Amy, Callum and TriThang.
The solution
It took an hour and a half – and a coffee break – but Nigel, Rhys and (independently) TriThang finally arrived at the same solution. The chance that each of the couples in my family draw each other’s names in our annual Secret Santa is 1 in 14,833, or about 0.007%.
However, it was Callum who came up with the answer the fastest. Recalling the topic of derangements that he learned nine years ago at university and encountered again in the final question of the 2016 year 12 NSW Extension 2 maths paper, he produced his solution:
Mathematicians working on the Kris Kringle problem together. From left to right: Nigel, Rhys, Sam, Amy, Callum and TriThang.
The solution
It took an hour and a half – and a coffee break – but Nigel, Rhys and (independently) TriThang finally arrived at the same solution. The chance that each of the couples in my family draw each other’s names in our annual Secret Santa is 1 in 14,833, or about 0.007%.
However, it was Callum who came up with the answer the fastest. Recalling the topic of derangements that he learned nine years ago at university and encountered again in the final question of the 2016 year 12 NSW Extension 2 maths paper, he produced his solution:
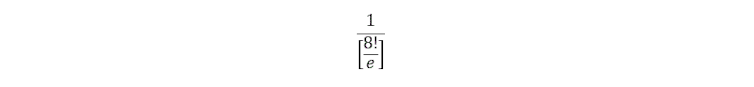 where the bottom line of this equation is just a particularly unusual way of writing 14,833 (the e refers to Euler’s number).
I was proud to finally reveal the solution to my brother: it was incredibly unlikely that all three partners would have drawn each other that night at dinner - about as unlikely as tossing a coin 14 times and coming up with 14 heads. However, he wasn’t quite as excited about knowing the answer as I was. (I told you my family aren’t particularly interested in maths.)
A Christmas twist
Here’s the thing, though: the Kris Kringle question is a known problem, related to the old hats problem. Why didn’t we just Google it?
Well, we all really enjoyed working on the problem. And Christmas is supposed to be fun. So I have to agree with Nigel when he asked: “Where is the fun in that?”
where the bottom line of this equation is just a particularly unusual way of writing 14,833 (the e refers to Euler’s number).
I was proud to finally reveal the solution to my brother: it was incredibly unlikely that all three partners would have drawn each other that night at dinner - about as unlikely as tossing a coin 14 times and coming up with 14 heads. However, he wasn’t quite as excited about knowing the answer as I was. (I told you my family aren’t particularly interested in maths.)
A Christmas twist
Here’s the thing, though: the Kris Kringle question is a known problem, related to the old hats problem. Why didn’t we just Google it?
Well, we all really enjoyed working on the problem. And Christmas is supposed to be fun. So I have to agree with Nigel when he asked: “Where is the fun in that?”
 Nigel (left) and Rhys solving the Kris Kringle problem on the whiteboard.
Thanks to all the mathematicians who worked on this problem, ACEMS for hosting the event that brought us together, and my family for coming up with the question.
Nigel (left) and Rhys solving the Kris Kringle problem on the whiteboard.
Thanks to all the mathematicians who worked on this problem, ACEMS for hosting the event that brought us together, and my family for coming up with the question.
Authors: Rheanna Mainzer, Melbourne Early Career Academic Fellow (Statistics Tutor), University of Melbourne
Read more http://theconversation.com/merry-christmaths-the-statistics-of-secret-santa-127730





